k-Hot Holographic Encoding

It's a fairly common thing in machine learning to need to deal with categorical data. Straightforwardly, if a model had to recognize inputs and classify them into lions, tigers, giraffes and scarecrows, we might assign lion=0, tiger=1, giraffe=2 and scarecrow=3. This is categorical data. A common way to encode this is with 1-hot encoding – this involves having a vector with a 1 representing a category and a 0 representing not-that-category. So lion would be encoded [1, 0, 0, 0], tiger would be encoded [0, 1, 0, 0], giraffe would be encoded [0, 0, 1, 0] and scarecrow [0, 0, 0, 1].

Things get more complicated when something might need to be represented by more categories than one. Let's say we had an animal that was a cross between a tiger and a lion – we might want to represent this as [1, 1, 0, 0]. Obviously this isn't one-hot encoding any more – we now have k-hot encoding, for some value of k.

Neural networks can be trained straightforwardly both with one-hot and k-hot encoding – they don't seem to mind. However, things get tricky when you have to deal with a very large number of possible categories. A popular approach to text analysis is bag-of-words – this involves analyzing a large amount of text, extracting its vocabularly, and creating vectors that include a 1 where a word is present in a piece of text, or 0 otherwise. In many languages, English particularly, order suprisingly word meaning effect little has. (Did you see what I did there, Yoda?)

Things get a bit tricky, though, because if you're doing text retrieval, it's often the rarer words that are the most useful. It's not uncommon to end up with very large vocabularies, bigger than 100000 words. Let's say we want to classify pieces of text taken from this vocabularly – if we wanted to train against, for example, Wikipedia's article classifications, there are also roughly that many of them. If we reject those that don't have many articles associated with them, we still have over 50000 of them if we insist on at least 1000 articles per category. Even a single dense layer gets painfully big at these dimensions – given 4 byte floats representing the weights, that's 20GB right there, without even considering the space needed to support backpropagation in training. Barely fitting a single layer into an NVIDIA A6000 means we need to do better.

A common technique is to throw away less common words from the vocabulary, but it's already known from text retrieval (back from the pre-neural networks are everything days) that this isn't a good idea. Similarly, we don't really want to throw away any categories we don't absolutely have to.

What we really want to be able to do is compress the words and categories into much shorter, more managable vectors, but without losing information or accuracy. Sounds impossible, but it isn't.

Let's say we have 100000 categories representing a bag-of-words, with a phrase size limit of (say) 200. We'd like to represent this as a k-hot vector that's managebly small, say with a size of 1024.

A simple way to attempt this would be to take the category ID and to wrap it around the vector however many times are necessary to fit everything in. So if c is the category ID, and we have a vector of size 1024, we could encode c as c % 1024 (where % is the integer modulo division operator). To a simplistic level, this actually does work, but it has the problem of aliasing (I'm borrowing the term here from digital signal processing). So, for example, if we want to encode the list of categories [1, 2, 95, 110, 250, 1000] and try to figure out from the encoding what categories we started with, we might get something like:

[1, 2, 28, 62, 95, 110, 250, 553, 559, ... , 99264, 99312, 99820]

This is actual output – the code uses another trick to improve the results rather than simple modulo arithmetic, but we'll get on to that later. The bad news is that this list has 587 elements, and any neural network using this data has absolutely no way to tell real encodings from aliases.

The trick turns out to be to represent categories with more than one '1' in the vector. Specifically, each category is encoded by exactly k '1' elements that are randomly positioned within the vector.

So if we take that same list and encode it with two '1' elements per category, we get

[1, 2, 95, 110, 250, 1000, 3696, 14934, 26553, 51130, 53643, 55596, 55903, 72592, 80631, 86806, 89631, 92838]

This is 18 elements, a huge improvement over 587, but we can do better. Setting three '1' values per category gives us

[1, 2, 95, 110, 250, 1000, 60663]

so just a single alias. Setting four '1's gives us

[1, 2, 95, 110, 250, 1000]

which is perfect reconstruction. These six categories are being encoded as 6 x 4 = 24 ones in the vector – still quite sparse.

It can be instructive to try this experimentally, varying the number of categories being encoded:

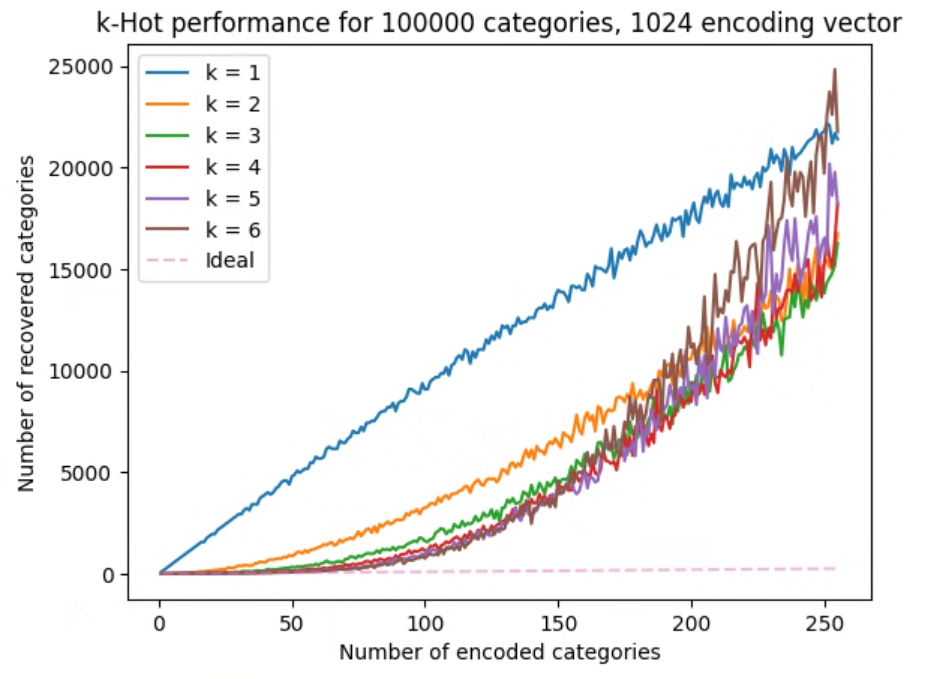
The graph shows what happens as you encode more and more categories into a fixed-size vector, here 1024 in length and assuming 100000 possible categories. The pink dashed line is what you'd get by encoding into a vector the size of the number of possible categories (generally impractical). The other lines showwhat happen as k varies. There is clearly no free lunch here, but even k = 2 vastly outperforms a naive wraparound modulo encoding. Zooming in on the bottom left is instructive:

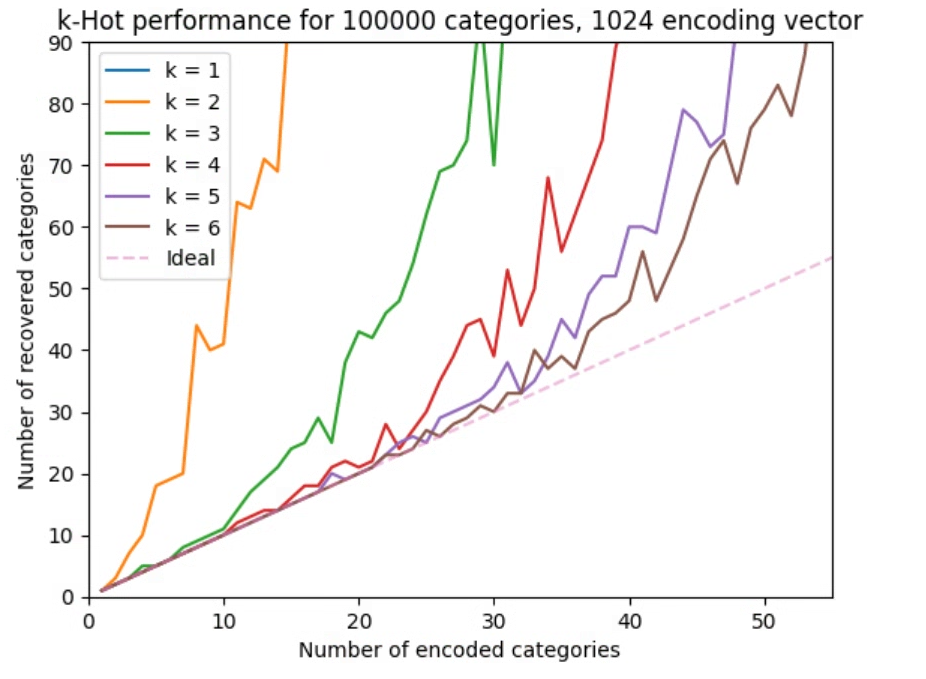
Up to 40 categories or so, it's clear that k = 6 does almost as well as ideal, which considering the 98:1 compression ratio is quite impressive. Of course, conventional data compression approaches will beat this ratio many times over, but the important factor here is that this encoding is very easy for subsequent neural network layers to extract useful information from.

If a neural network needs to uniquely identify a category in order to improve its loss function (which is not actually always necessary), it needs to encode the equivalent of a logical AND function. This is very straightforward for a dense layer with a relu activation function, and will easily fall out of training.

Recovering encoded categories

I've talked a lot about how categories are encoded, so it's a good idea to also mention how they can be decoded. We've talked about using these encodings to drive the inputs of neural networks – they can also be used to train their outputs.

I recommend that if you try this, you use an output layer with a sigmoid activation function (don't use softmax, they only work for 1-hot). You should also probably use binary-crossentropy as an error function. This will result in the outputs of the neural network roughly corresponding to probabilities.

To unpack these probabilities, the following algorithm will achieve this:

for i in [0 .. num_categories]:
m = 1.0
for p in [0 .. k]:
m = m * vec[ permutation[p, i] ]
cat[i] = m ^ (1/k)

where num_categories is the number of categories, vec is the encoded vector, cat is the recovered categories, and permutation[p, i] is an array of permutation matrices that map category numbers onto indices into vec, where each row of the array is a different set of permutations.

If we start by assuming the values in vec are probabilities in the range [0 .. 1], we use multiplication like the probabilistic equivalent to logical AND. This passes through 0 and 1 unchanged, but values like 0.5 get squashed toward zero as k increases, so we take the k-th root of the result to undo the effects of the multiplications.

This approach makes it possible to use an output vector for a classifier that has a size that is a small fraction of the number of possible categories. This works in neural network training because the elements that each category are mapped to are individually trained by backpropagation, and upwind dense layers can and will implement the necessary logical structures.

Kind of seems holographic, doesn't it?

It's a similar principle – encoding a large, sparse data set into a short vector by creating something a bit like different paths a photon can pass down, then allowing them to interact and entangle.

I'm currently attempting to use this to build a very small, lightweight text classifier that is extremely fast, of the order of a millisecond or so to process a piece of text. I'm training a variant with about 42 million parameters that seems to work fairly well. This is a direct requirement for Euravox, because whilst there are probably way more reliable classifiers out there, we have a requirement to do as much as we can with as little hardware as possible, and as low a power footprint as possible. Whilst the current buzz would have us chuck huge numbers of big GPUs at the problem and use far larger models, even LLMs, this doesn't fit either our needs or ethos. I'm definitely not up for paying a third party for tokens. And in any case, LLMs royally suck at text classification, I know, I've tried.

Open source implementation

I have a simple Python implementation of the encoder/decoder that I'm happy to release. I've not done so yet, but I'll have some time waiting for training runs to complete in the next few days, so watch this space. I'll edit the web version of this post to include a link, and will probably write a new post announcing a repo.

A personal note

I've spent most of the last 20 years being unable to publish without jumping through excessively painful hoops. It is an absolute breath of fresh air to just be able to write anything I like now!